实时渲染中的抗锯齿(一): 采样理论
前言:抗锯齿在图形渲染领域是一个经久不衰的话题,由于显示设备分辨率有限,应用程序对于高模,高分辨率贴图的渴求,锯齿问题也是图形应用程序经常会遇到的问题。 锯齿问题对于视觉效果的影响显著,根据不同的原因也产生了各种各样的抗锯齿方法。笔者根据自己的实际工作经验,对常见的抗锯齿算法进行一些简单总结, 欢迎各位读者交流讨论,如有纰漏,欢迎指正。
由于锯齿问题本质上还是信号处理中的混叠问题,所以这一片开头的文章首先对采样理论相关内容做一下简单回顾。
奈奎斯特-香农采样理论 (Nyquist–Shannon sampling theorem)
傅里叶变换 (Fourier-Transform)
物理世界中的信号一般都是连续信号,我们表示为$s(t)$,在信号处理系统中,分析输入信号的频率组成(频谱分析)一般是非常重要的,这一般是通过对输入信号进行傅里叶变换信号来进行时域↔频域的转换。傅里叶变换的公式如下。[Wikipedia 傅里叶变换]
\[F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-i \omega t} \, dt\]信号系统中常见的函数及其傅里叶变换如下:
| 时域函数 | 频谱函数 | 图示 | 描述 |
|---|---|---|---|
| Impulse | Constant | 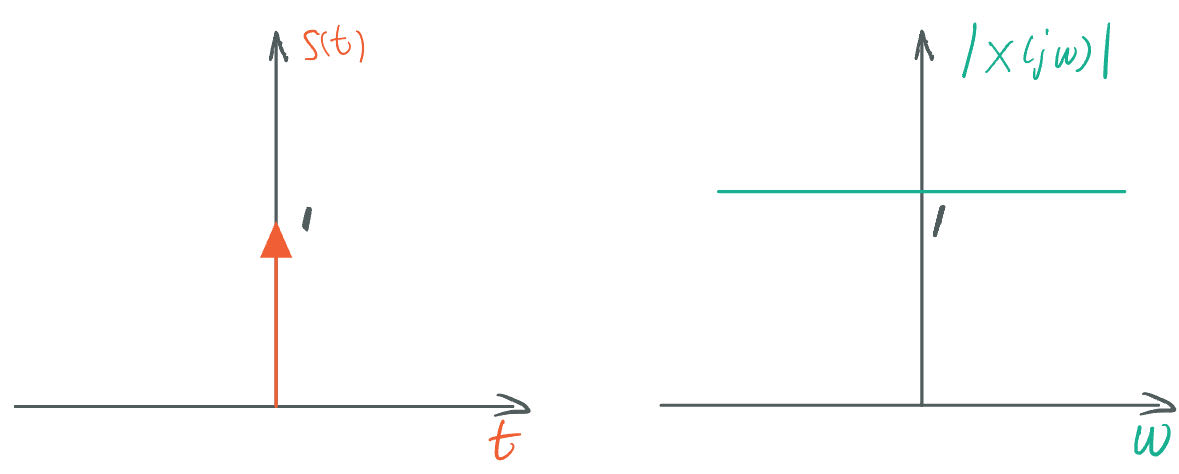 |
(在原点)脉冲函数与常数函数互为傅里叶变换,不在原点的脉冲函数的傅里叶变换为一次函数 |
| Dirac Comb | Dirac Comb | 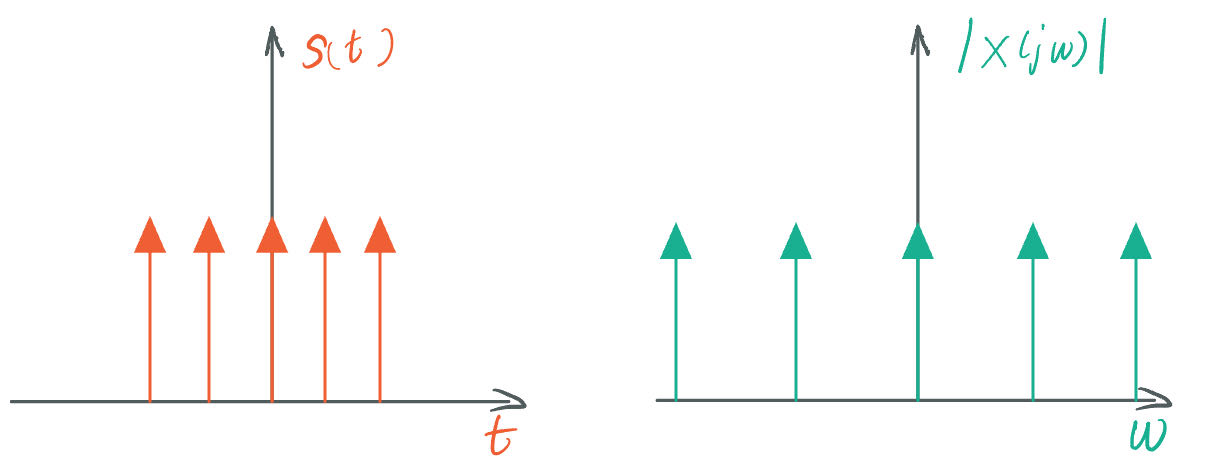 |
狄拉克梳函数的傅里叶变换仍然是狄拉克梳函数,二者间距成反比 |
| Rect Window | Sinc | 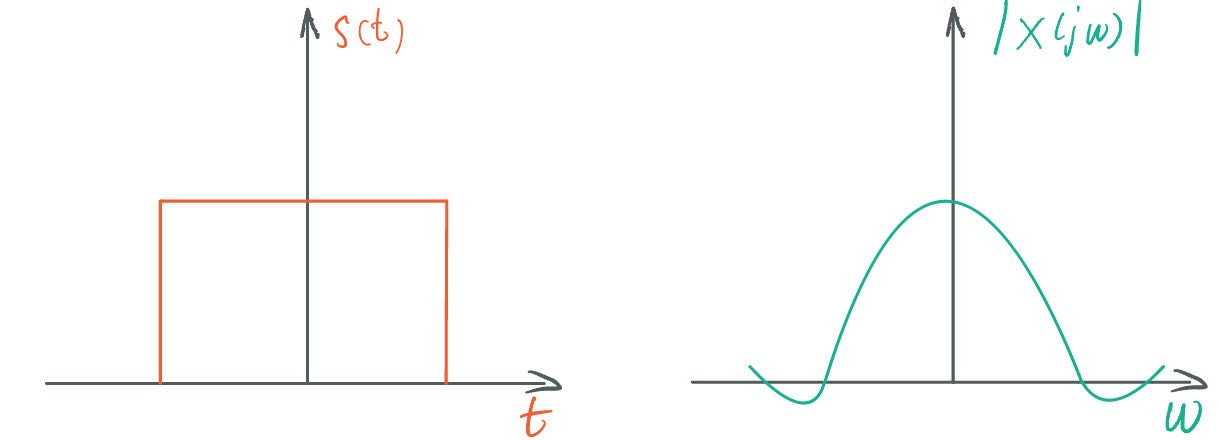 |
矩形窗函数与 Sinc 函数互为傅里叶变换 |
| Gaussian | Gaussian | 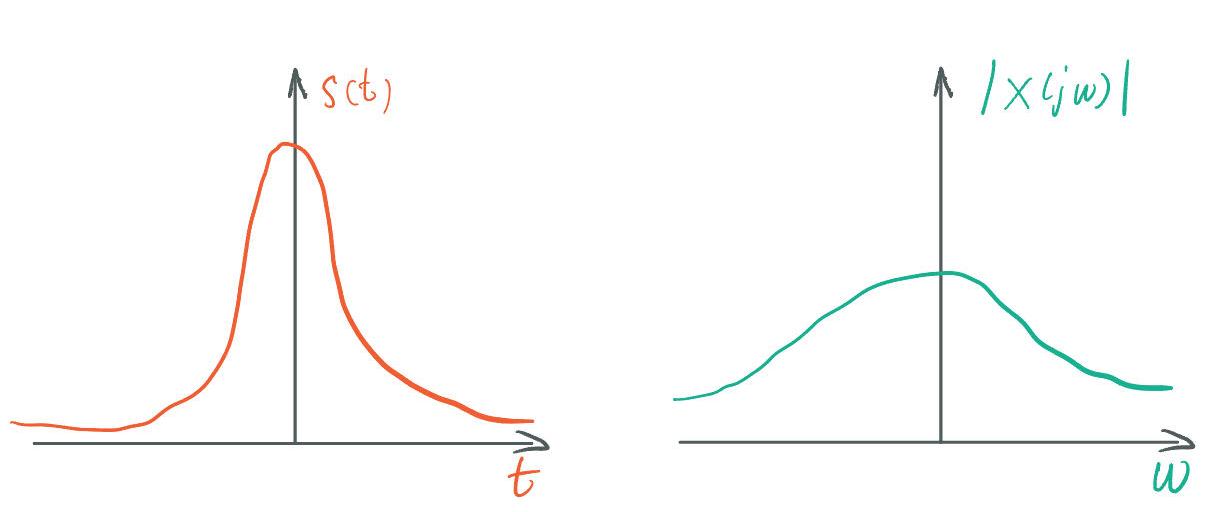 |
高斯函数的傅里叶变换仍然是高斯函数, 二者方差成反比 |
卷积操作 (Convolution)
卷积是两个信号的一种运算形式,在信号系统的频谱分析中比较常见,两个信号的卷积运算公示如下。 [Wikipedia 卷积]
\[(f * g)(t) = \int_{-\infty}^{\infty} f(\tau) g(t - \tau) \, d\tau\]以下一些较为重要的的规律:
- 对两个函数在时域上进行乘积操作,等价于对这两个函数在频域上进行卷积操作,反之亦然。
- 一个函数与脉冲函数(无论是否在原点的脉冲)的卷积,等价于在脉冲函数的位置重建该函数(需要考虑脉冲的幅值)。
- 卷积操作具有线性性质,满足交换律,结合律。所以输入函数与一个梳函数的卷积等价于输入函数与梳函数所有脉冲分量的卷积结果之和
- 梳函数的傅里叶变换仍然是梳函数,时域的梳函数间隔与其对应的频域梳函数的间隔成反比。
- 两个高斯函数的卷积仍然是高斯函数,结果的方差是两个输入方差之和
- 频谱函数关于原点对称,这个结论比较直观
一个函数与脉冲函数时域的卷积等价于二者傅里叶变换频域的相乘,而脉冲函数的频谱为一次函数,最终结果相当于在脉冲出重建该输入函数。 上述规律均可通过傅里叶变换和卷积操作证明得到。
混叠问题 (Aliasing)
对于一个时间信号系统 $s(t)$,采样操作通常是,每隔一段时间(采样间隔)对原始信号进行一次采样(乘积操作),得到一个离散的结果,然后用这些离散结果还原出原始信号。这个过程相当于对原始信号 $s(t)$ 与一个采样梳函数 $f(t)$ 进行乘积操作,如下图所示。
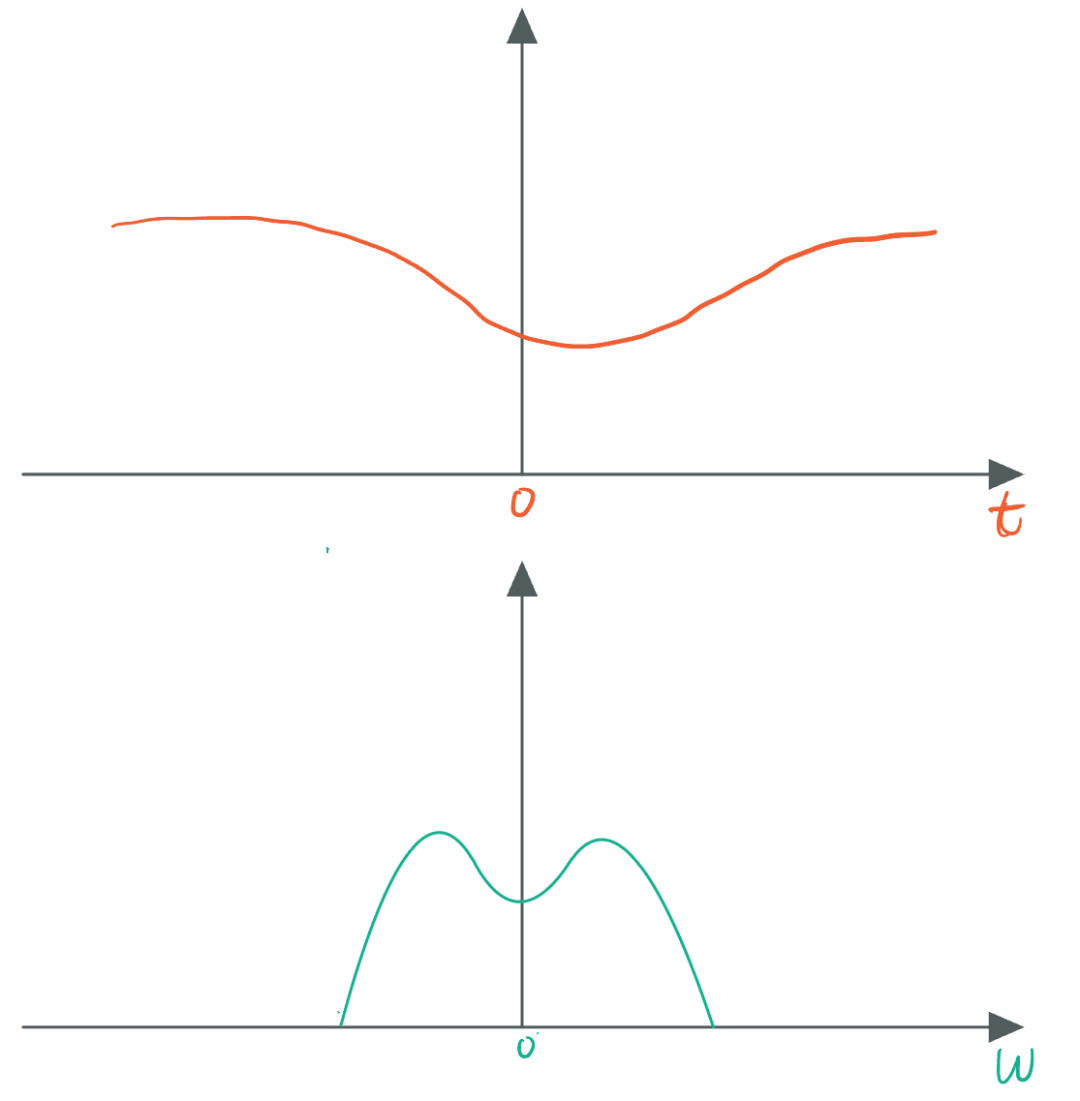
这等价于对原始信号的频谱函数 $S(\omega)$ 与 梳函数的频谱函数 $F(\omega)$ 进行卷积操作,如下图所示。
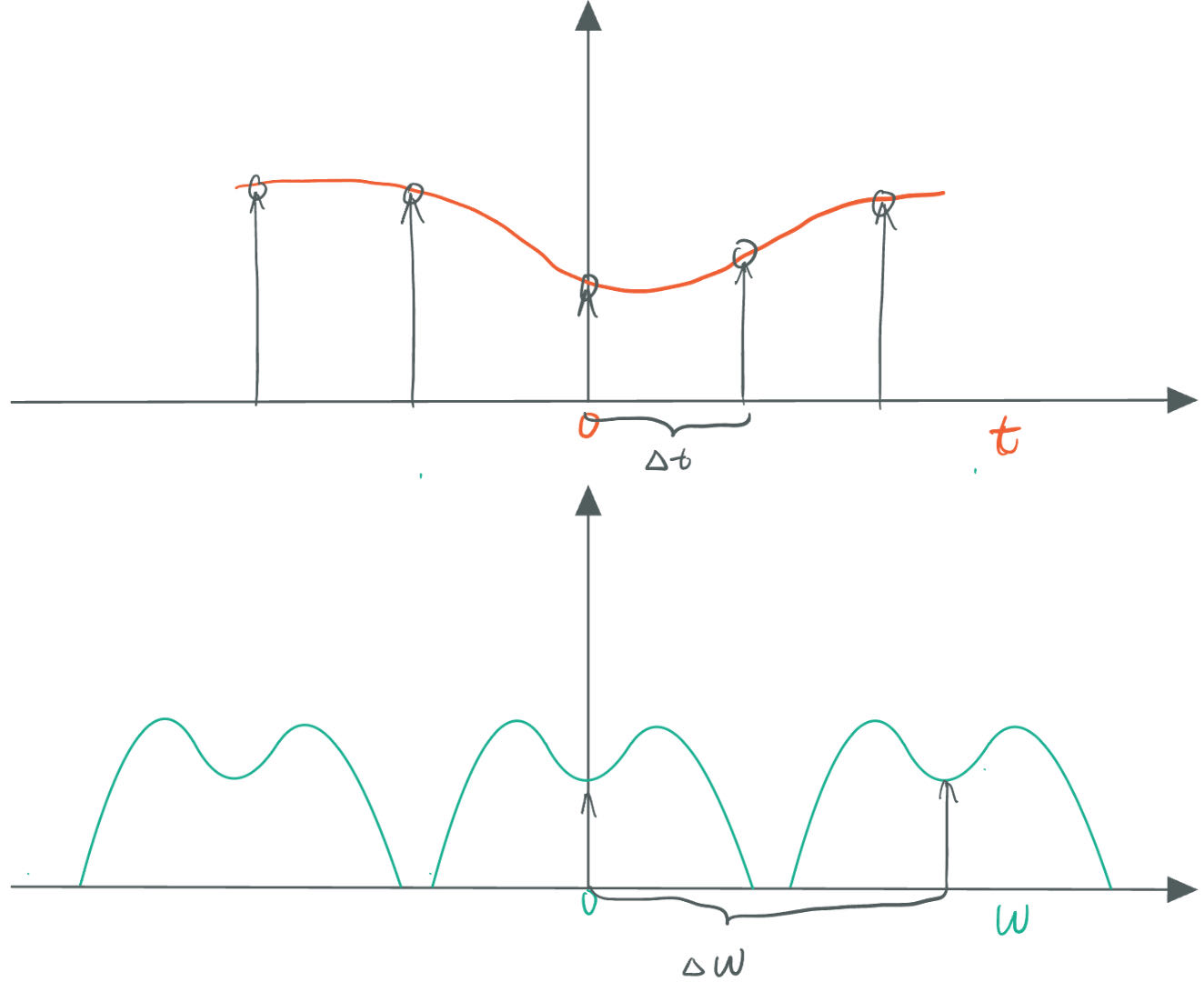
由于梳函数的傅里叶变换仍然是梳函数。在频域二者的卷积结果如上图。上图并未出现混叠,在频域中,频谱函数并未出现重叠现象。我们已知输入信号的频谱函数具有对称性,最大频率为$\omega_{max}$,当$\Delta \omega < 2 * \omega_{max}$时,频谱函数会互相重叠,这就是混叠(Aliasing),混叠会使得在原始的时间域上无法通过采样得到的数值重建正确的输入函数,从而造成失真。上述介绍的原始函数以时间t为自变量,当原始函数的自变量为空间坐标时,混叠也会造成空间上的失真现象。
无论是时间维度上的采样还是空间维度上的采样,混叠现象都会有十分明显的视觉错乱,常见的有:
- 人眼观察汽车车轮高速旋转,会发现“车轮反转”(时间)
- 用手机对显示器屏幕进行拍照而产生的摩尔纹 (空间)
采样定理
根据上述结论,为了避免失真,必须满足$\omega_{max}$,当$\Delta \omega > 2 * \omega_{max}$,也就是采样频率必须大于原始信号中最高频率的2倍,才能保证二者在频域中的卷积不会发生函数重叠,也就是才能避免混叠(Aliasing)。
采样定理非常简单,对于已经出现的混叠现象,所有的一切补救行为,都是围绕着采样定理,包含两个方向:
- 对原始函数进行低通滤波,过滤高频信号
- 提高采样频率,以达到采样定理的要求
滤波
假设原始信号函数为$s(t)$,滤波函数为$g(t)$,滤波操作即为对$s(t)$和$g(t)$进行卷积操作,这在频域上相当于对二者的傅里叶变换之后的频谱函数进行乘积操作。根据前文描述,我们想要过滤掉原始信号中的高频信息,这代表了我们理想中的低通滤波器在的频谱函数是一个频域中的窗函数。频域中的窗函数在时域中是不规则的。这表明在时域中的滤波核会不规则,增大计算复杂度。不过我们可以以此评判滤波函数。比如详见的时域滤波函数有:
- 矩形窗函数:加权平均,计算简单;但是频谱函数中会漏高频信息,滤波质量差。
- 高斯函数:高斯核需要有一定大小,计算复杂,但是频谱较好
- 其他窗函数:矩形窗、汉宁窗、汉明窗和布莱克曼窗 [Wikipedia 窗函数]
本博文内容为作者原创,转载请注明出处并附上原文链接,感谢支持与理解。
